Autor

Dr Zvonko Rakarić

Aktivne fasade na zgradama predstavljaju jedan od mogućih načina povećanja iskorišćenja ambijentalne energije, u odnosu na „pasivne“ ili statičke fasade. Aktivne fasade karakteriše mogućnost promene njihovog oblika ili nekih njihovih karakteristika u toku određenih delova dana ili godine. Na ovaj način je moguće prilagoditi fasadu zgrade uslovima koji će što efikasnije doprineti iskorišćenju ambijentalne energije, kao što su energija sunca, vetra, vibracija različitog porekla …  Istovremeno, ovakve fasade treba da zadrže i ne naruše sve prethodne važne karakteristike statičkih fasada, kao što su estetski izgled, termička i zvućna izolacija, fizička zaštita i slično.

Kao poseban izazov ovakvom prilazu je implementacija elemenata aktivne fasade na postojeće, već izgrađene objekte. Pri tome je potrebno da sa ovakvim fasadama  bude zadovoljeno: estetsko uklapanje objekta u njegovo okruženje, minimiziranje  dodatnog opterećenja postojeće strukture, jednostavnost montaže i upravljanja, pouzdanost i trajnost, efikasno iskorišćenje i „prikupljanje energije – energy harvesting” itd.

Slika 1. Zgrada kampusa Univerziteta Salermo, Italija. (slika preuzeta sa: https://www.sciencedirect.com/science/article/pii/S1359836816320960)

 

U studiji predstavljenoj u [1] koja je navedena na kraju ovog teksta, grupa istraživača je predložila aktivnu fasadu u vidu tensegriti strukture i njenu primenu predvidela na zgradi kampusa Univerziteta u Salermu (Slika 1). Tensegriti strukturu karakterišu  elementi kao što su štapovi, i fleksibilni zategnuti elementi (kablovi, opruge i slično). Međusobnom kombinacijom ovih elemenata i njihovim opterećenjem, pre svega deformacijom fleksibilnih elemenata se mogu postići različite željene stabilne ravnotežne konfiguracije. Istovremeno se može postići laka konstrukcija, a koja može imati relativno veliku nosivost. Neki smatraju da ovakve konstrukcije  predstavljaju “strukture budućnosti” [2].

Navedene karakteristike ovih struktura predstavljaju i neke od razloga opravdanosti njihove primene u aktivnim fasadama. Pored male mase i relativno velike čvrstoće, tu je i mogućnost upravljanja ovakvim strukturama. Kao što je već i pomenuto, promenom deformacije fleksibilnih elemenata se utiče na željenu ravnotežnu konfiguraciju i njenu izmenu, a što predstavlja mogućnost prilagođavanja fasade zgrade u odnosu na date spoljašnje uslove.

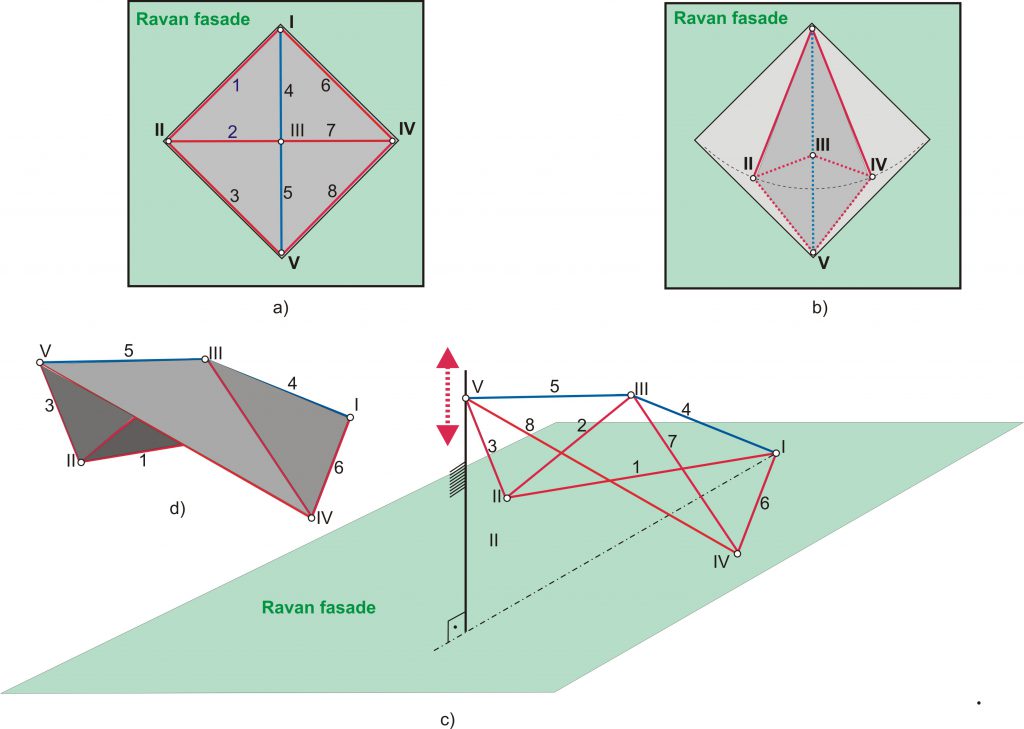
Slika 2. Mehanizam modula tensegriti strukture

Izgled fasade sa tensegriti strukturom koju je osmislila pomenuta grupa istraživača [1] je prikazana na slici 1a) – zatvorena kofiguracija; 1b)- polu otvorena konfiguracija.

Osnovna jedinica ili moduo ovakve tensegriti strukture je prikazana na Slici 2.  Na slici 2a) je prikazana struktura u zatvorenoj konfiguraciji (struktura zatvara kvadratni otvor na fasadi zgrade) u ravni fasade. Nju čini osam elemenata (numerisani od 1-8), 6 štapova, prikazani crvenim linijama i dva fleksibilna (uvek) zategnuta elementa koji su predstavljeni plavim linijama. Štapovi su međusobno vezani zglobno u čvorovima koji su na slici označeni rimskim brojevima (I-V). Svi čvorovi su pokretni, osim čvora I koji predstavlja jedinu nepokretnu tačku ove strukture. Primenjujući kinematsku analizu na ovu konstrukciju (bez fleksibilnih elemenata 4 i 5), uočava se da je ovakva struktura pokretljiva. Ako za trenutak zamislimo da se radi o ravanskom problemu, odnosno da se elementi konstrukcije mogu kretati samo u ravni fasade i da se zglob V može kretati po nepokretnoj vođici u pravcu I-V, tada ovakva struktura ima jedan stepen slobode kretanja {SSK=6[elemenata]x3[SSK štapa u ravni]-8[zglobova]x2[broj ograničenja zgloba]-1[pokretni oslonac]x1[broj ograničenja pokretnog oslonca]=1, videti [3]). Znači, jezikom klasične analize konstrukcija,  ovakva struktura bi se zvala mehanizam. Ovde treba imati u vidu činjenicu da fleksibilni elementi 4 i 5 ne utiču na kinematsku pokretljivost neke strukture i ne treba ih smatrati za elemente “kinematskog” mehanizma. Vrednost SSK=1 ukazuje da su na osnovu poznavanja položaja jednog od elemenata mehanizma, tada definisani u potpunosti položaji svih ostalih elemenata. Razmatranje ravanskog problema je ovde samo uvod, radi lakšeg razumevanja prostornog problema, budući da se u ovom slučaju razmatrana realna struktura može kretati u prostoru. Na Slici 2b) je prikazana projekcija razmatrane strukture u nekoj proizvoljnoj prostornoj konfiguraciji (Slika 2c), na ravan fasade. Elementi koji su predstavljeni punim linijama se u ovoj projekciji vide u pravoj veličini (elementi 1 i 6). Ostali elementi zauzimaju određeni položaj u prostoru i zaklapaju sa ravni fasade uglove koji su različiti od nule, u ovoj projekciji se ne vide u pravoj veličini i predstavljeni su isprekidanim linijama.

Znači, u ovom slučaju se ne radi o ravanskoj, već o prostornoj konstrukciji. Konstrukciono je omogućeno da se čvor V kreće po vertikalnoj nepokretnoj vođici koja je normalna na ravan fasade (Slika 2c). U slučaju ovakve prostorne konstrukcije, sada postoje dva stepena slobode kretanja (6×5-8×3-2×1-1×2=2, videti [3]). Prilikom razmatranja kinematike ovog prostornog mehanizma je pretpostavljeno da je međusobna rotacija između svih elemenata omogućena putem sfernih zglobova. Kao posledica da je SSK=2, je ta da je sada moguće zadati dva nezavisna kretanja, odnosno pomeranja posmatrane konstrukcije-mehanizma.  Ovde je to pre svega od značaja za čvorove III i V koji se sada mogu nezavisno kretati (pomerati) jedan u odnosu na drugi. Budući da su između ovih čvorova, kao i između čvora III i I postavljeni fleksibilni elementi, tada se sa zadavanjem položaja (kretanja) čvorova III i V definišu deformacije fleksibilnih elemenata, odnosno aksijalne sile zatezanja u njima, i konačno, na takav se način definišu ravnotežne konfiguracije ove tensegriti strukture. Pri analizi ravnotežnih konfiguracija se razmatraju ravnoteže pojedinih čvorova za konkretnu geometriju, uzimanjem u obzir svih elemenata, i štapova i fleksibilnih elemenata. Uz pomoć odgovarajućih softvera, ovakva analiza je značajno olakšana.

Konačno, treba reći i to da su između elemenata ove strukture mogu postaviti četiri fleksibilna površinska elementa oblika trougla (Slika 2d ili slika 3). To mogu biti fleksibilni solarni paneli i/ili platna koja mogu imati ulogu zaklona od sunca ili ulogu “jarbola” a putem kojih se onda može koristiti energija vetra. Ovo poslednje je moguće, kako su autori ove studije naveli, tako što se pod dejstvom vetra fleksibilni linijski elementi deformišu, a što se onda na različite načine može koristiti za proizvodnju električne energije, putem odgovarajućeg generatora, piezolektričnim elementima itd. Takođe, moguće je koristiti i fenomen nelinearnih oscilacija deformabilnog tela u struji fluida-efekat flatera ili lepršanja. Ideju za ovo su autori studije [1] dobili na osnovu patenta [4] čiji je naziv “blinking sail windmill”  za koji se tvrdi da ima veliki stepen iskorišćenja energije vetra. Od značaja je mogućnost promene ravnotežne konfiguracije ove strukture, jer se na taj način omogućuje da solarni paneli budu pod odgovarajućim uglom u odnosu na položaj sunca, a što direktno utiče na stepen iskorišćenja sunčeve energije.

Slika 3. 3D model

Kao što se na osnovu predstavljenog može videti, za osmišljavanje, projektovanje i konstruisanje sličnih struktura je potrebno razumeti, između ostalog: mehaničke modele, mehanički sistem i opisivanje i ocenu ravnoteže ravanskih i prostornih sistema, kinematsku analizu, pojam veza i uticaja na pokretljivost sistema, način definisanja položaja i kretanja i njihovo povezivanje sa aksijalnom deformacijom elemenata,  razumevanje linearnih i nelinearnih problema u smislu geometrijske nelinearnosti, razumevanje i uticaja inertnosti elemenata, razumevanje problema oscilacija elemenata, kako sa stanovišta negativnih efekata, tako i sa stanovišta korišćenja oscilacija ovakvih struktura na “prikupljanje” ambijentalne energije… Naravno, ovo je samo deo potrebnog predznanja, da bi se uspešno mogle realizovati ovakve strukture, kao što smo već i pomenuli, po nekima, strukture budućnosti.

dr Zvonko Rakarić

vanredni profesor UNO Mehanika

Fakultet tehničkih nauka Novi Sad

Reference:

[1]   Composite solar facades and wind generators with tensegrity architecture, 2017

https://www.sciencedirect.com/science/article/pii/S1359836816320960)

[2]       Tensegrity – Structural system for the Future, Rene Motro, Butterworth-Heinemann, 2003.

[3]     “Kinematika i dinamika sa ilustrativnim primerima iz strukturalnog inženjerstva”-Glava 4: stepen slobode kretanja, Zvonko Rakarić, udžbenik u pripremi, http://www.ftn.uns.ac.rs/n1920040582/

[4]     Blinking sail Windmill https://patents.google.com/patent/US7780416