Autor

dr Zvonko Rakarić

Graditeljski poduhvat s početka 21 veka, Milau vijadukt na jugu Francuske, završen pre 13 godina, i dalje pleni pažnju i interesovanje. Po mnogo čemu prvi i jedinstven građevinski objekat, prilikom čije je izgradnje  ostvareno više rekorda  i dobijeno više prestižnih nagrada i priznanja. Mnogo je o ovom vijaduktu napisano i objavljeno.  U ovom testu ću naglasak staviti na ono što je prilikom izgradnje bilo i najkompleksnije, a što je posebno  interesantno i sa stanovišta inženjerske mehanike. A to je postavljanje dve mostovske ploče teške desetine hilada tona na sedam vitkih stubova, više od dve stotine metara iznad reke Tarn.

Slika 1. Dolina reke Tarn i Milau vijadukt

Da izgledom vijadukt ne naruši ambijent predivne doline koju treba da premosti, a istovremeno  da bude dovoljno čvrst da se nosi sa silama prirode i opterećenjima tokom korišćenja, je ono čime se vodio prilikom osmišljavanja ovog graditeljskog remek dela, čuveni arhitekta britanac Norman Foster. Izgled mosta, koji treba da  ostavi utisak lakoće, elegantnosti i nenametljivosti na okolinu, je pred inženjere postavio brojne izazove. Dolinu široku dva i po kilometra je vijadukt trebao “dodirnuti”, samo u sedam tačaka. I tih sedam stubova je trebalo da budu izutetno  vitki, a debljina ploče mosta što tanja.

Slika 2.

Željeni estetski izgled i ispunjavanje svih kriterijuma koje jedna ovakva struktura mora da zadovolji su međusobno isprepletene i vidljive u svakom njenom detalju. Pomenuću samo neke od njih. Naprimer,  u gornjem delu se stubovi račvaju na dve grane (Slika 2). Ovo grananje, zajedno sa pilonom koji se na njega nadovezuje, oblika okrenutog slova Y, tvori fascinantan vizuelni efekat, ali istovremeno  ima i veliki značaj po statičku i dinamičku stabilnost.

Konstrukcija mosta je kontinualna na osam polja sa višestrukim strukturama sa kosim zategama (multi cable-stayed bridge), bez mogućnosti ankerisanja pilona  sa obale. Zbog predela u kojem se nalazi, kao i velike visine, morale su biti predviđene opsežne studije o dejstvu vetra na nju. Ovo su samo neke od specifičnosti koje ovaj vijadukt čine izuzetno interesantnim sa statičkog i dinamičkog stanovišta strukturalnog inženjerstva, kao i sa stanovišta inženjerske mehanike,  čemu ću posvetiti neki drugi tekst.

Ovde ću se, kao što sam pomenuo, fokusirati na problem postavljanja mostovskih ploča. Nakon što su stubovi vijadukta bili sagrađeni (Slika 3a), sledilo je postavljanje mostovskih ploča (Slika 3b), pilona, kablova itd.

Projektom je bilo predviđeno da se ploče mosta izrade izvan samog mesta vijadukta, a zatim da se na određeni način postave na most. Ovo je podrazumevalo  “navoženje”  dve ploče mosta, svaka sa jedne strane doline, na stubove mosta. Pri tome, zbog izrazite vitkosti stubova, pretila je relna opasnost da dođe do njihovog oštećenja, i urušavanja (Slika 3c).

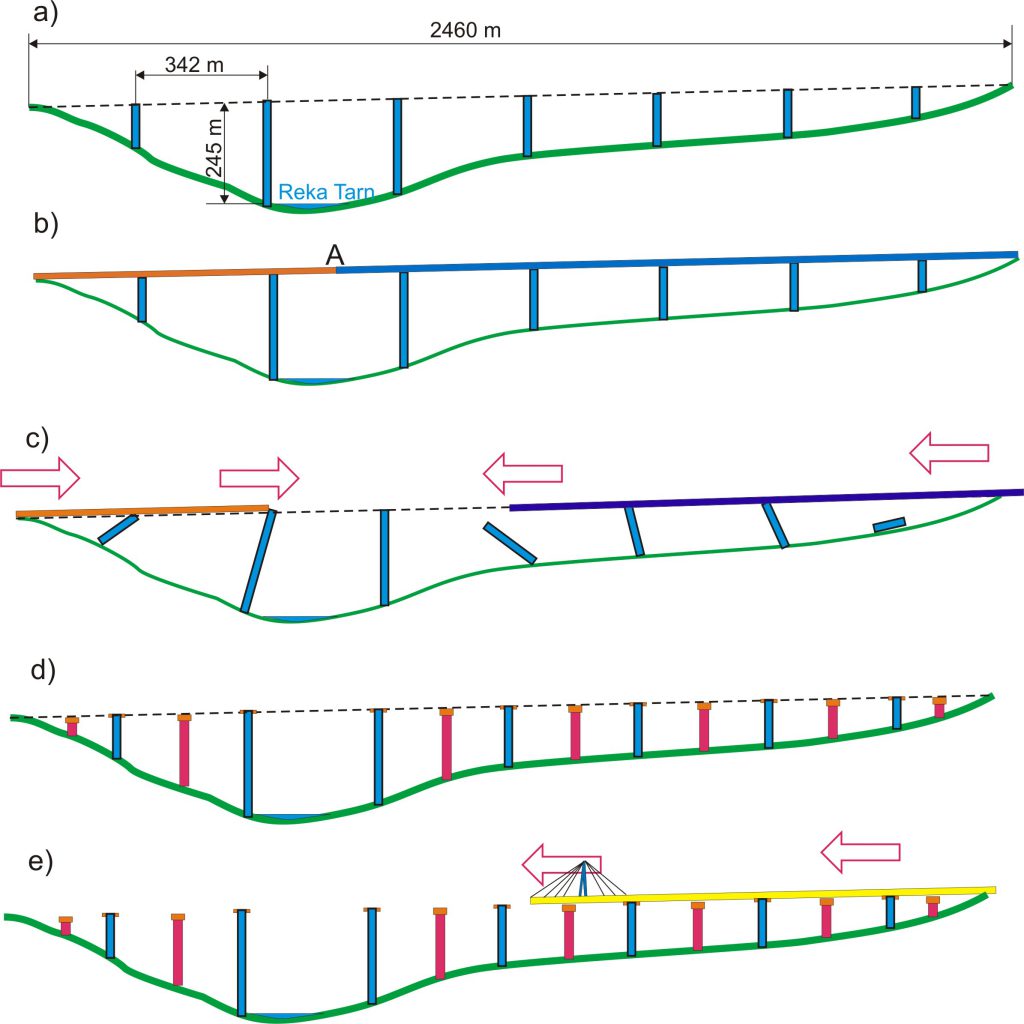
Slika 3

Ovaj problem je interesantno razmotriti sa stanovišta inženjerske mehanike. Naime, ovo se može opisati jednostavnim mehaničkim modelom prikazanim na Slici 4.  Telo I je postavljeno na sto (element II) i nekom spoljašnjom silom F se izaziva njegovo pomeranje po stolu. Ukoliko su noge stola (elementi III) dovoljno elastični, može, pod određenim uslovima doći do njihovog savijanja. Razlog za ovu deformaciju je sila trenja koja se kao unutrašnja sila javlja između tela (I) i površine stola (II), a koja se zatim prenosi na noge stola kao poprečna sila savijanja. Primenivši pravilo dekompozicije sistema tela, ovo je prikazano na Slikama 4 b) i c). Treba naglasiti da se ovde pretpostavlja da se prilikom kretanja sistema zanemaruju inercijalne sile. Zanemarivanje inercijalnih sila u odnosu na druge sile koje se javljaju se može primeniti, između ostalog,  u slučaju da su ubrzanja elemenata sistema mala. Naprimer, u slučaju kretanja ploče mosta vijadukta pomeranje  je iznosilo 600 mm u toku 4 minute, ostvarene su male brzine, i što je važnije, mali intenziteti ubrzanja. No, kao što se vidi, ma koliko male da su vrednosti brzine, a pre svega ubrzanja, sile trenja postoje.

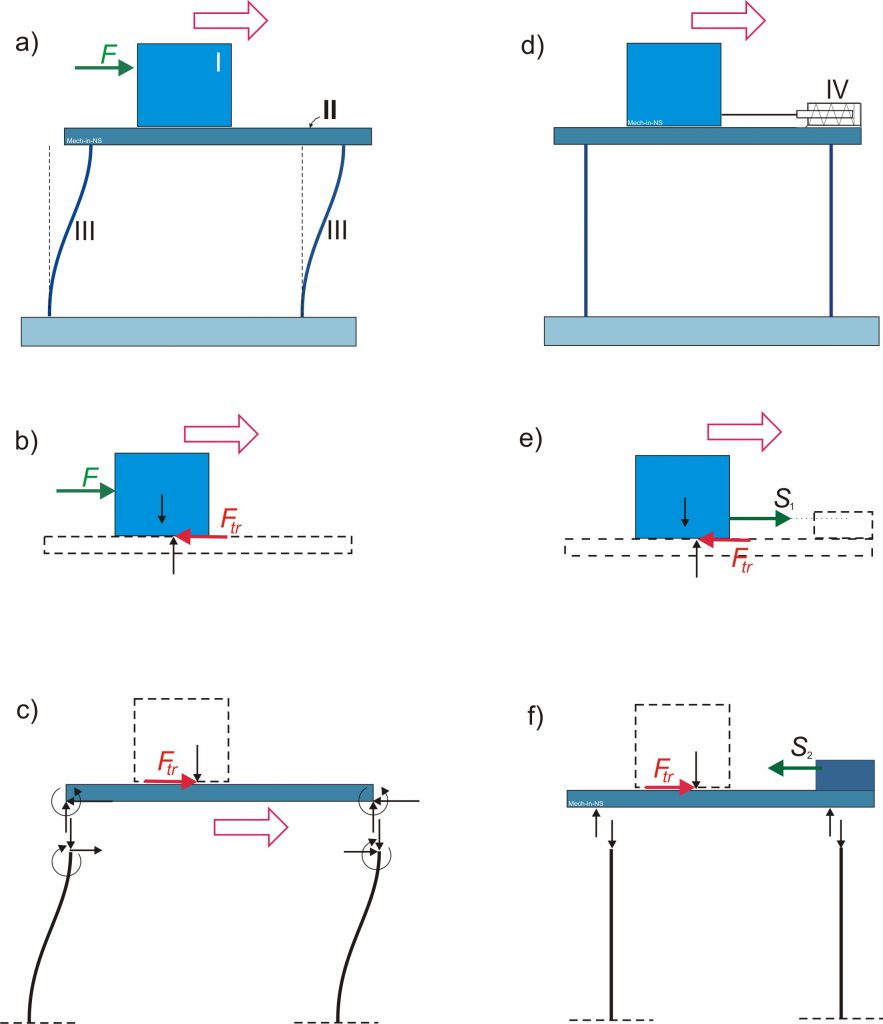
Slika 4.

Poništavanje dejstva sile trenja na elastične elemente i samim tim i sprečavanje njihovog savijanja se može ostvariti tako što se aktivna sila potrebna za pomeranje tela I po telu II generiše ne izvan, već unutar posmatranog sistema.  Konstruktivno, to je moguće, naprimer, postavljanjem nekog pogonskog elementa  IV (elektromotora, pneumatskog ili hidrauličkog cilindra itd…) koji je fiksiran za površinu stola, i direktno deluje na element I, kako je prikazano na Slici 4d). Na ovaj način elementi II i IV čine jedno telo. Na slikama 4 e) i f) su prikazani elementi ovakvog sistema nakon dekompozicije.  Zbog ovako ostvarenog pogona elementa I, javljaju se unutrašnje sile S1 (dejstvo pogonskog elementa na element  I)  i unutrašnja sila S2 (dejstvo elementa  I na element II). Kao što je prikazano na Slici 4f) sila trenja koja dejstvuje na element II je sada kompenzovana sa silom S2 tako da nema generisanih poprečnih sila na noge stola, koje sada ostaju u vertikalnom položaju.

Na ovome što je prethodno opisano se zasniva i metod koji je iskorišćen prilikom postavljanja ploča na stubove mosta. U tom cilju je pored postojećih sedam stalnih, postavljeno i sedam privremenih stubova (na slici 3d su označeni crvenom bojom). Zatim su na vrhovima stubova  postavljeni posebni uređaji (Slika 3e), nazvani “translatori” sa kojima je ostvareno translatorno pomeranje mostovskih ploča po stubovima.  Na vrhu svakog stuba je postavljeno po četiri ovakva uređaja (Slika 6a). Rad svih translatera je sinhronizovan kompjuterski, obezbeđujući na taj način translatorno pomeranje ploče mosta. Osnovu funkcionisanja “translatora” čine dva prizmatična elementa I i II oblika klina, koji naležu jedan na drugi (Slika 5). Na slikama 6 je prikazana suština funkcionisanja translatera, sa stanovišta inženjerske mehanike.

Slika 5. Princip strme ravni za pokretanje mostovskih ploča

Dodirne površine ova dva elementa preko kojih elementi relativno kližu jedan u odnosu na drugi su presvučene teflonom (koeficijent trenja teflon-teflon je u rangu koeficijenta trenja čelik-led). Pokretanje elementa I i II se ostvaruje sa hidrauličkim cilindrom HC1 I HC2, respektivno (Slika 6a). Pomeranje ploče se vrši u ciklusima. Svaki ciklus traje oko četiri minute i može se podeliti na tri nezavisna dela, prikazana na Slikama 6 b), c) i d). Tokom svakog ciklusa se ploča mosta pomeri 600 mm u horizontalnom pravcu. Na slikama je proizvoljno izabrana tačka B elementa II u cilju jasnijeg sagledavanja kretanja. Takođe je na stubu mosta izabrana i nepokretna tačka O. Kretanje tačaka u odnosu na nju je apsolutno kretanje.

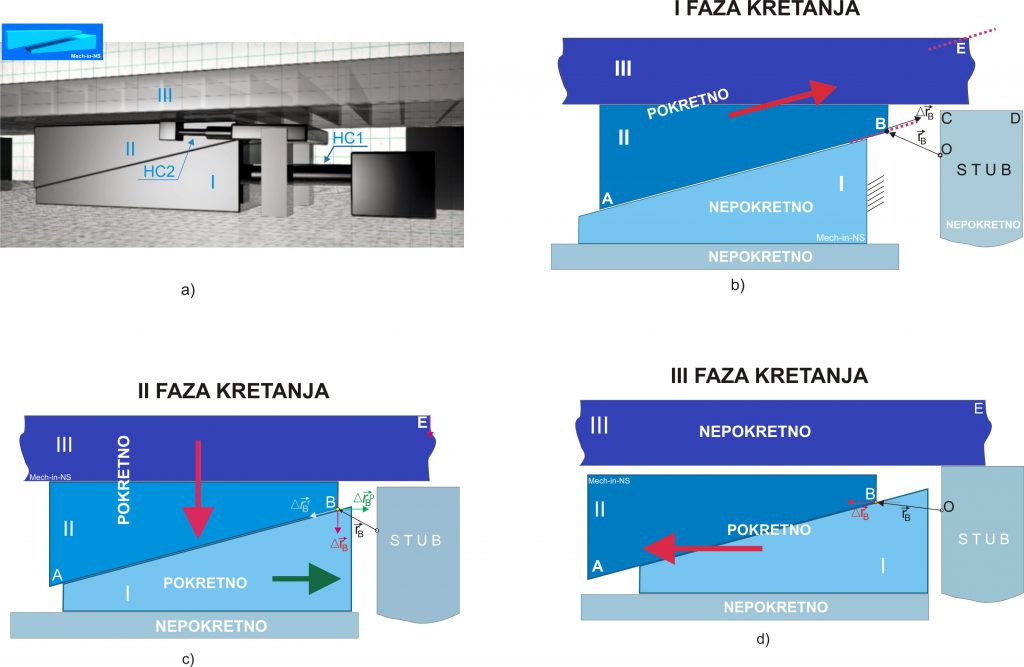
Slika 6. Faze kretanja “translatera”

Prvi deo ciklusa: Element I je nepokretan. Element II klizi po elementu I i kreće se zajedno sa pločom (III) translatorno u pravcu i smeru koji je prikazan debljom crvenom strelicom. Na Slici 6b) je prikazan vektor položaja tačke B, kao i vektor pomeranja tačke B.

Drugi deo ciklusa: Nakon što je element II (kao i cela ploča) došao do gornjeg zaustavnog položaja, u kretanje se dovodi element I u pravcu i smeru zelene horizontalne strelice (ovo je prenosno kretanje-p). Istovremeno se relativno (r) u odnosu na element I kreće i element II. Kombinacijom ova dva kretanja, ostvareno je apsolutno kretanje elementa II (a sa njim i ploče mosta) vertikalno naniže. Ovim kretanjem se ploča mosta spušta na stubove. U cilju još boljeg razumevanja ovog dela kretanja, može se posmatrati kretanje, naprimer, tačke B.

Treći deo kretanja: Ploča mosta je nepokretna i leži na stubovima. Elementi I i II se zajedno, kao jedno telo kreću u pravcu i smeru horizontalne crvene strelice i dolaze u početnu poziciju za novi ciklus.

Među drugim brojnim problemima koje su inženjeri morali rešavati tokom postavljanja ploča, ovde ću navesti još samo jedan od njih. Tokom pomeranja ploče duž stubova, uvek je jedan deo ploče bio prepušten na poslednjem stubu do kojeg se stiglo (Slika 7). Da se ne bi narušila stabilnost celokupne još uvek nepotpuno učvršćene konstrukcije, postavljen je pilon sa kablovima. Zategnutost kablova je neprestano bila proveravana i menjana u skladu sa pomeranjem ploče i trenutnim opterećenjem. Pri tome su neki od kablova bili tek neznatno zategnuti, tako da je prilikom dejstva vetra moglo doći do njihovih vibracija. Takve vibracije kablova kao elastičnog kontinuuma bi se prenele na konstrukciju, a što se moralo sprečiti. Stoga su, poprečno na postojeće kablove, za njih vezani pomoćni kablovi (Slika 7) koji su na takav način uneli malo prigušenje u oscilatorni sistem, i istovremeno uticali na krutost kao i na odgovarajuću modalnu frekvenciju kablova.

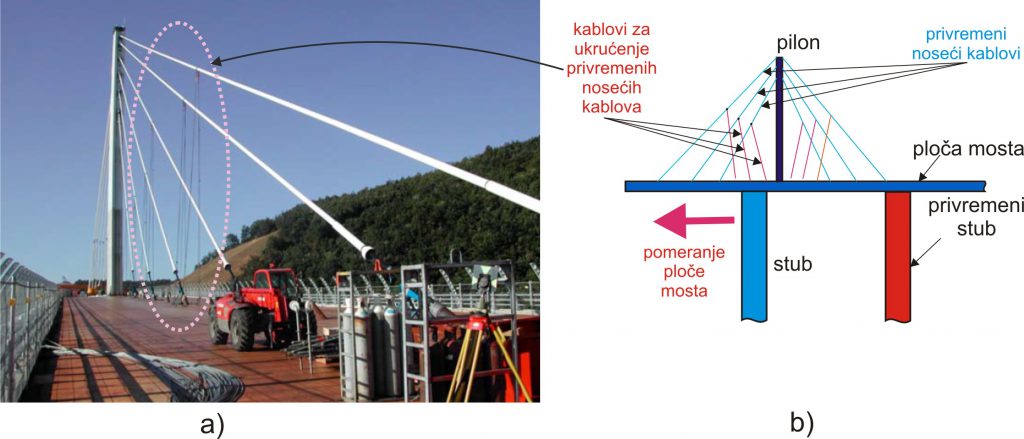
Slika 7. Sprečavanje oscilacija kablova tokom montaže ploča

Kao što se može uočiti, dobro poznavanje osnova inženjerske mehanike je bilo od izuzetne važnosti prilikom opisanih aktivnosti na postavljanju mostovskih ploča. Ovde su, upravo s namerom opisane takve aktivnosti kroz koje mogu biti uočeni elementi koji se izlažu u osnovnim delovima Inženjerske mehanike: statike, otpornosti materijala (mehanike deformabilnog tela), kinematike i  dinamike. Konačno, interesantno je i pomenuti i to da, kao što su verovatno i graditelji egipatskih piramida koristili strme ravni prilikom pokretanja i podizanja teških blokova, isti osnovni princip su ovde iskoristili i francuski graditelji. Principi mehanike su uvek isti, i takvi će i ostati.

dr Zvonko Rakarić

vanredni profesor UNO Mehanika

Fakultet tehničkih nauka Novi sad

zvonko@uns.ac.rs